Final Project 1: Image Quilting

Part 1: Randomly Sampled Texture

Overview

In this section, we implemented the quilt_random function, which generates an output image of a specified size out_size by randomly sampling square patches of size patch_size from a given texture sample. The function begins tiling the output image from the upper-left corner, placing randomly selected patches until the image is filled. If the patches do not perfectly fit the dimensions of the output image, the remaining edges are left as black borders. While this method is straightforward and computationally efficient, it obviously produces visible seams and lacks coherence between adjacent patches, resulting in a less realistic texture.

Results

Below we present some examples of using the quilt_random(sample, out_size, patch_size). Parameter choices are out_size = 300 and patch_size = 25 consistently. We see that out of these textures, the only one that looks reasonably good when randomly quilted is grass.jpg. The explanation is simple: grass has the fewest edge artifacts and seams of all the images, hence was the easiest to quilt. This trend continues throughout the project: Textures with less dominant seams and edges are easier to quilt (and texture transfer).

Initial Brick Texture (from paper)

Generated by Random Quilting

Initial Cloth Texture (from paper)

Generated by Random Quilting

Initial Grass Texture (from Google)

Generated by Random Quilting

Initial water Texture (from Google)

Generated by Random Quilting

Initial text Texture (from paper)

Generated by Random Quilting

Part 2: Resolving Overlapping Patches using SSD

Overview

The function quilt_simple generates an output image of size out_size by arranging patches of size patch_size. The process begins with a randomly selected patch for the upper-left corner. Subsequent patches are sampled to overlap with existing patches. For example:

• The second patch along the top row overlaps horizontally by overlap pixels.
• Patches in the first column overlap vertically by overlap pixels.
• Other patches overlap both horizontally and vertically.

The cost of placing each patch is computed, and a random patch is chosen from the lowest tol samples. This is done with two helpers:

1. ssd_patch

This function calculates the cost of a patch using the sum of squared differences (SSD) between the overlapping regions of the existing output and the sampled patch:

                            ssd_cost = ((M*T)**2).sum() - 2 * cv2.filter2D(I, ddepth=-1, kernel=M*T)
                                 + cv2.filter2D(I**2, ddepth=-1, kernel=M) 
                                

2. choose_sample

This function selects a patch based on the cost map from ssd_patch. It identifies patches with the lowest costs and randomly chooses one from the top tol smallest costs. For debugging, setting tol=1 ensures that the patch with the absolute lowest cost is always chosen, resulting in a near-exact copy of the input texture. Higher tol gives more variability and stochasticity to the texture generated.

Results

Below we present some examples of using the quilt_simple(sample, out_size, patch_size). Parameter choices are out_size = 300 and patch_size = 25 consistently.

The results show a marked improvement over the quilt_random approach, but some seams and artifacts remain noticeable in specific images. This is particularly apparent in textures with strong edges, such as bricks_small.jpg or text_small.jpg, where the quilting process encounters greater challenges in achieving smooth transitions.

An intriguing aspect of the algorithm is how minimizing the sum of squared differences (SSD) enables it to "understand" the importance of aligning edges. High-contrast regions, like edges, act as dominant outliers under an \( L^2 \) norm and drive the matching process. For instance, in the generated texture, the seams between bricks are mostly well-aligned, reflecting the influence of SSD optimization. In contrast, an earlier bug in the code, which caused ssd_patch to select random invalid patches, resulted in poorly aligned seams, emphasizing the importance of proper patch selection.

While these results approach optimality, the visible seams to the naked eye highlight the limitations of this method. In the next section, introducing a minimum cut technique addresses these issues.

Initial Brick Texture (from paper)

Generated by Optimal-SSD Overlap Quilting

Initial Cloth Texture (from paper)

Generated by Optimal-SSD Overlap Quilting

Initial Grass Texture (from Google)

Generated by Optimal-SSD Overlap Quilting

Initial water Texture (from Google)

Generated by Optimal-SSD Overlap Quilting

Initial text Texture (from paper)

Generated by Optimal-SSD Overlap Quilting

Part 3: Resolving Seams using Min-Cut

Overview

To address the edge artifacts caused by overlapping patches, the next step incorporates seam finding into the texture synthesis process. The process utilizes the cut function from utils.py, which determines the minimum-cost contiguous path from one side of a patch to the other, based on a cost map (bndcost). The cost of a path through each pixel is calculated as the squared differences (summed across RGB channels for color images) between the overlapping regions of the output image and the newly sampled patch. For horizontal paths (left overlaps), the function works directly, while for vertical paths (top overlaps), the transposed cost map can be used (cut(bndcost.T).T).

If a patch has both top and left overlaps, two seams must be computed—one for each overlap. The final mask is defined as the intersection of the masks generated by each seam, using np.logical_and(mask1, mask2).

To illustrate the process, we include a visualization for a selected patch, highlighting the following steps:

• (a) The two overlapping RGB portions: the patch already in the output image (template) and the newly selected patch.
• (b) The per-pixel SSD cost of the overlapping region, masked by the template mask.
• (c) The binary horizontal mask indicating which pixels are retained from the new patch versus the existing template.
• (d) The binary vertical mask for the same purpose, applied to the vertical seam.
• (e) The final combination mask created by intersecting the horizontal and vertical masks.

Results

Here, we use patch_size = 25, out_size = 600, and overlap = 5. Following the guidelines provided in the paper, we approximately choose overlap = patch_size // 5. The purpose of increasing the first two parameters is to produce more visually appealing results. This ensures that any color inconsistencies (as blending is not yet applied) are less noticeable. Additionally, a larger patch size provides more patches, giving the texture pattern more flexibility to synthesize high-quality information. It also makes the individual blocks less discernible.

However, for the water texture, we use out_size = 300. This is because water lacks significant edges or abrupt color changes that might appear odd without blending from nearby regions.

Observations on the Min-cut Path

Comparison with Other Methods

Brick

Initial Brick Texture (from paper)

Generated by Random Quilting

Generated by SSD Quilting

Generated by Min-cut Quilting

Cloth

Initial Cloth Texture (from paper)

Generated by Random Quilting

Generated by SSD Quilting

Generated by Min-cut Quilting

Grass

Initial Grass Texture (from google)

Generated by Random Quilting

Generated by SSD Quilting

Generated by Min-cut Quilting

Water

Initial Water Texture (from google)

Generated by Random Quilting

Generated by SSD Quilting

Generated by Min-cut Quilting

Text

Initial Text Texture (from paper)

Generated by Random Quilting

Generated by SSD Quilting

Generated by Min-cut Quilting

Part 4: Texture Transfer

Overview

The texture transfer method builds on the quilt_cut function to synthesize a new texture that not only mimics the source texture's appearance but also aligns with a target image's structure or pattern. This technique is guided by a pair of images: sample, which serves as the source for patch sampling, and a guidance_im, which defines the structure that the synthesized texture must follow.

The key difference between texture_transfer and quilt_cut is the inclusion of an additional cost term that evaluates the difference between the source patch and the target image at the location being synthesized. This added cost ensures that the output texture aligns more closely with the features of the target image. The total cost for a patch is a weighted sum of:

• The cost of aligning overlapping regions (as in quilt_cut).
• The cost of matching the source patch to the target image.

The parameter \( \alpha \) can be adjusted to balance how much the output prioritizes matching the target image versus preserving the texture pattern of the sample.

Results

In implementing texture_transfer, careful tuning of parameters was essential for achieving realistic results:

1. Output Size and Patch Parameters:
   out_size was set to 600, with patch_size values of 25 or 15 and corresponding overlap values of 5 or 3, respectively.
   • Increasing overlap often made the textures appear unnatural.
   • Using larger patches (patch_size) highlighted seams, while smaller patches required more computation and occasionally resulted in unrealistic textures.
2. Alpha:
   The blending weight alpha was set to 0.2, which worked well for smoothing overlapping regions.
3. Tolerance:
   tol was set to 2, allowing little variability in patch selection. While higher tol values introduced greater texture variety, they occasionally produced unwanted variability that disrupted the desired image (e.g., selecting unsuitable patches for the target structure). This is because there are likely few patches that work well.

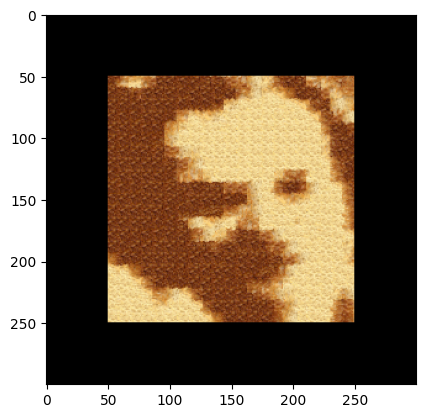
Texture transfer was generally more effective with target images containing fewer edges, as fewer constraints made the synthesis process simpler. However, an absence of edges also reduced contrast, making it harder to recreate features. For example, the blend of water and Newton has few edge details.

On the other hand, blends with distinct edges performed better, though the implementation often made the patch blocks more visible. This suggests that an iterative approach—starting with larger patches and progressively refining with smaller patches—could significantly improve results. Similarly, incorporating advanced blending techniques could further reduce visible seams, as explored in the "Bells & Whistles" section.

Feynman in Cloth Texture

Feynman in Sand Texture

Feynman in Toast Texture

Feynman in Grass Texture

Jasprit Bumrah in Grass Texture

Newton in Water Texture

Bells and Whistles: Face in Toast (Image Quilting + Laplacian Blending)

Overview

In this section, we explore the use of blending and quilting techniques for texture transfer. Our goal was to fix the challenge of placing Feynman's face onto a toast texture. While the results are mostly disappointing, some promising directions were identified. Below are the optimal parameters used during experimentation:

• Quilting: out_size = 600, patch_size = 20, overlap = 5, tol = 3
• Blending: depth = 4, sigma = 2, skip = 2
• Alpha Range: \( 0.20 \le \alpha \le 0.45 \), suitable for naive texture transfer.

1. The most promising result was achieved using naive texture transfer combined with Laplacian blending and a mask at the end. This method shows the potential to produce better results, though limitations in the Project 2 (Laplacian Blending) code made the outcomes less satisfactory. I think averaging the brightness and color contrast of the source and target images could significantly enhance blending.

2. Texture transfer with patch-wise blending worked surprisingly well for reconstructing Feynman's face while removing texture oddities. However, the block seams remained too visible. This issue arises because the blending process lightens the overlapping patch while darkening the non-overlapping regions, leaving a noticeable disparity.

3. To address the visible seams, a 2D Gaussian blur was applied to the overlapping borders. While this reduced seam visibility, it resulted in noticeably thicker and still distinguishable seam regions. This suggests that while blurring helps with smoothing, it may require more sophisticated techniques to truly integrate the patches seamlessly.

Based on the results, the following improvements can likely be made:

• Brightness and Contrast Adjustment: Prior to blending, equalizing the brightness and contrast of the source and target images may create a more cohesive blend.
• Advanced Seam Blending: Explore methods like multiscale blending or adaptive masking to better integrate overlapping regions and reduce visible seams.
• Iterative Refinement: Experiment with iterative approaches to progressively refine the blend, starting with coarse adjustments and moving to finer details.
• Fourier Transforms: This is more just a thought, but I think Fourier Transform Methods as in the class could be particularly helpful in implementing texture transfer. This is because as seen with minimizing SSD, we can rephrase image quilting as an edge alignment problem. This can be resolved by decomposing into high and low frequencies.

Texture Transfer Standard

Feynman

Toast

Standard Texture Transfer

Texture Transfer with Patch-wise Blending

Feynman

Toast

Standard Texture Transfer

Texture Transfer with Patch-wise Blending and Corner Blurring

Feynman

Toast

Standard Texture Transfer

Texture Transfer with overall Blending only

Feynman

Toast

Texture Transferred Feynman with Mask

Standard Texture Transfer